Tématem tohoto článku je výpočet polykarbonátového vrchlíku vlastními rukama. Musíme se naučit, jak vypočítat hlavní parametry konstrukce spojené s její pevností a rozměry. Tak pojďme.

Co počítáme
Musíme se naučit počítat:
- Tloušťka polykarbonátu a rozteč přepravky v závislosti na očekávaném zatížení sněhem na metr čtvereční.
- Rozměry krytu oblouku (což z hlediska geometrie spadá do výpočtu délky oblouku).
Pro upřesnění: zkoumáme způsoby, jak vypočítat oblouk pro známý poloměr a úhel sektoru, stejně jako pro případ, kdy známe pouze vzdálenosti mezi krajními body povrchu oblouku.
- Minimální průřez potrubí se známým ohybovým zatížením.
V tomto pořadí budeme pokračovat.
Tloušťka soustružení a povlaku
Začněme výpočtem zatížení sněhem.
Než přijdeme na to, jak vypočítat polykarbonátový vrchlík, zformulujeme několik předpokladů, na kterých je výpočet založen.
- Uvedené údaje jsou relevantní pro vysoce kvalitní materiál bez známek destrukce ultrafialovým zářením. Polykarbonát bez UV filtru křehne po 2-3 letech provozu na světle.

- Záměrně zanedbáváme omezenou deformační stabilitu přepravky, považujeme ji za absolutně pevnou.
A nyní - tabulka, která vám pomůže vybrat optimální tloušťku polykarbonátu a rozteč přepravky.
| Zatížení, kg/m2 | Rozměry buňky přepravky s tloušťkou polykarbonátu, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050x790 | 1200 x 900 | 1320 x 920 | 1250x950 |
| 900x900 | 950x950 | 1000x1000 | 1100x1100 | |
| 820x1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880 x 660 | 1000x750 | 1050x750 | 1150x900 |
| 760 x 760 | 830 x 830 | 830 x 830 | 970x970 | |
| 700 x 860 | 750 x 900 | 750x950 | 850x1050 | |
| 200 | 800x600 | 850x650 | 950 x 700 | 1100x850 |
| 690x690 | 760 x 760 | 780 x 780 | 880 x 880 | |
| 620x780 | 650x850 | 700x850 | 750x950 | |
Oblouk
Výpočet podle poloměru a sektoru
Jak vypočítat oblouk pro vrchlík, když známe poloměr ohybu a obloukový sektor?

Vzorec bude vypadat takto P=pi*r*n/180, kde:
- P je délka oblouku (v našem případě délka polykarbonátové desky nebo profilové trubky, která se stane prvkem rámu).
- pi je číslo „pi“ (ve výpočtech, které nevyžadují extrémně vysokou přesnost, se obvykle bere rovno 3,14).
- r je poloměr oblouku.
- n je úhel oblouku ve stupních.
Pojďme jako příklad vypočítat vlastními rukama délku oblouku vrchlíku s poloměrem 2 metry a sektorem 35 stupňů.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 metru.
V procesu práce často nastává opačná situace: je nutné upravit poloměr a sektor oblouku na pevnou délku oblouku. Důvody jsou jasné: cena polykarbonátu je dostatečně vysoká, aby minimalizovala množství odpadu.
Je zřejmé, že v tomto případě bude součin sektoru a poloměru roven P/pi*180.
Zkusme oblouk osadit pod standardní plech o délce 6 metrů. 6/3,14*180=343,9 (se zaokrouhlením). Dále - jednoduchý výběr hodnot s kalkulačkou v ruce: například pro obloukový sektor 180 stupňů můžete mít poloměr rovný 343,9 / 180 \u003d 1,91 metru; s poloměrem 2 metry bude sektor roven 343,9 / 2 \u003d 171,95 stupňů.
Výpočet po akordech
Jak vypadá výpočet návrhu polykarbonátového vrchlíku s obloukem, pokud máme informaci pouze o vzdálenosti hran oblouku a jeho výšce?
V tomto případě se uplatňuje tzv. Huygensův vzorec. Abychom to použili, duševně rozdělme tětivu spojující konce oblouku na polovinu, poté nakreslíme kolmici k tětivě uprostřed.
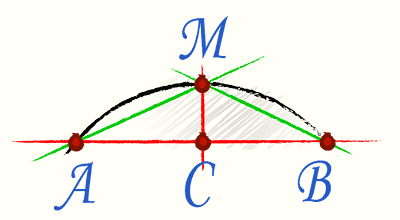
Samotný vzorec má tvar Р=2l+1/3*(2l-L), kde l je akord AM a L je akord AB.
Důležité: výpočet poskytuje přibližný výsledek. Maximální chyba je 0,5 %; čím menší je úhlový sektor oblouku, tím menší je chyba.
Vypočítejme délku oblouku pro případ, kdy AB \u003d 2 ma AM - 1,2 m.
P=2*1,2+1/3*(2*1,2-2)=2,4+1/3*0,4=2,533 metrů.
Výpočet průřezu se známým ohybovým zatížením
Docela životní situace: součástí vrchlíku je hledí známé délky. Můžeme na něm zhruba odhadnout vrcholné sněhové zatížení. Jak vybrat profilovou trubku takového úseku pro nosníky, aby se při zatížení neohýbala?

Poznámka! Záměrně se nedotýkáme toho, jak vypočítat zatížení vrchlíku. Hodnocení zatížení sněhem a větrem je zcela soběstačné téma na samostatný článek.
K výpočtu potřebujeme dva vzorce:
- M = FL, kde M je ohybový moment, F je síla působící na konec páky v kilogramech (v našem případě hmotnost sněhu na hledí) a L je délka páky (délka nosníku, který nese zatížení od sněhu, od okraje k bodu upevňovacích prvků) v centimetrech.
- M/W=R, kde W je moment odporu a R je pevnost materiálu.
A jak nám tato hromada neznámých hodnot pomůže?
Samo o sobě nic. Pro výpočet chybí některá referenční data.
| třídy oceli | Pevnost (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15 GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Odkaz: Oceli St3, St4 a St5 se obvykle používají pro profesionální trubky.
Nyní, na základě údajů, které máme, můžeme vypočítat moment ohybového odporu profilové trubky. Pojďme to udělat.
Předpokládejme, že se na dvoumetrovém vrchlíku se třemi nosnými nosníky z oceli St3 nahromadí 400 kilogramů sněhu.Pro zjednodušení výpočtů se dohodneme, že celé zatížení dopadne na hranu hledí. Je zřejmé, že zatížení každého nosníku bude 400/3=133,3 kg; s dvoumetrovou pákou bude ohybový moment roven 133,3 * 200 \u003d 26660 kgf * cm.
Nyní vypočítáme moment odporu W. Z rovnice 26660 kgf * cm / W = 2100 kgf / cm2 (pevnost oceli) vyplývá, že moment odporu by měl být alespoň 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Jak nás hodnota momentu odporu přivede k rozměrům potrubí? Prostřednictvím sortimentních tabulek obsažených v GOST 8639-82 a GOST 8645-68 regulujících rozměry čtvercových a tvarových trubek. Pro každou velikost označují odpovídající moment odporu a pro obdélníkový úsek - podél každé z os.
Po kontrole tabulek zjistíme, že minimální rozměr čtvercové trubky s požadovanými charakteristikami je 50x50x7,0 mm; obdélníkový (s vertikální orientací větší strany) - 70x30x5,0 mm.

Závěr
Doufáme, že jsme čtenáře nepřetěžovali množstvím suchých čísel a vzorců. Jako vždy další informace o metodách výpočtu a návrhu polykarbonátových přístřešků naleznete ve videu v tomto článku. Hodně štěstí!
Pomohl vám článek?